The first segment of this module contains an example of the use of a Mathlet to organize group work by students in a lecture setting. This second segment provides samples of what you can ask groups of students to do using Mathlets, inside or outside a classroom. Each segment is followed by questions, my remarks about the lecture fragments and the features of Mathlets, and examples that demonstrate their use. At the end there are a couple of exercises.
1. In this module…
You will first try out the Mathlets in a separate window. Next, you will watch video lectures where you will be instructed to pause and engage in a variety of activities, as well as think about the questions posed.
- Download Mathlets in Group Work Slides [ PDF, 1.9MB ]
- Watch Mathlets in Group Work, Module 2 Video
2. Learning Objectives
After completing this module, the participant will be able to use Mathlets to:
- Encourage group work in the classroom.
- Encourage genuine mathematical reasoning by students.
- Provide a focus for small group projects.
3. Segment 1: Mathlets in Group Work
Module 1 Mathlets in Lecture discussed the use of Mathlets during in-class lectures. One advantage to using Mathlets is the ability to allow students to explore and learn collaboratively as they complete problems and projects. This module will introduce the use of Mathlets in group work by providing a recorded example from a teachers workshop.
Launch
Mathlet: Isoclines
Transcript [ PDF ]
3.1 Activity
Think About: Isoclines
- Did you find my image of the slope field as a field of grass knocked down by the wind helpful? And how about the small animal running through it, as an image of an integral curve?
- Suggest one other way in which I could have gotten the students working with each other using Isoclines.
- What are your comments about the Isoclines Mathlet. Could some part of this be useful in one of the classes you teach?
Segment 1 Review
Below, you will find:
- Lecture Fragment Topics
A listing of the topics covered by the lecture fragment
- Lecture Components
A listing of the components of the lecture fragment
- Discussion and Questions
Dr. Miller’s reflection on this lecture fragment
- Further use of the Isoclines Mathlet
Further ideas of things one can do with the Isoclines Mathlet in a classroom group work setting.
Lecture Fragment Topics
- Direction fields and integral curves
- Isoclines, nullcline
- Fences, entrapment of integral curves
Lecture Components
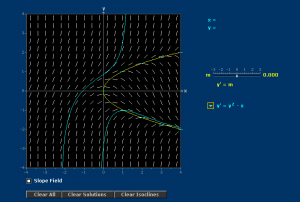
- Slope field hay field
- Integral curves deer tracks
- Where do extreme points occur?
- Talking with students
- Gathering students for an answer
- Showing isoclines
- Group discussion about maxima vs minimum
Consider
My casual cursor drag, generating a whole family of solutions, was carefully rehearsed. If I had dragged carelessly the integral curves would have jumped abruptly, confounding the impression I wished to give that the solutions formed a smoothly changing family of functions.
 I left 90 seconds for the participants to think about where the extrema of solutions of this differential equation were. Was that enough time? I checked up on the work of two or three groups. Should I have looked in on more?
I left 90 seconds for the participants to think about where the extrema of solutions of this differential equation were. Was that enough time? I checked up on the work of two or three groups. Should I have looked in on more?
Did you notice my gesture of where the nullcline was? It was reversed from how it looked to the audience! I still have not learned that skill.
Clearly students wanted to keep working on things themselves in this segment!
Then I asked the question about why the extrema are maxima. In retrospect, I should have asked the participants to work on this on their own.
Note that I systematically talked about what I was doing with the Mathlet. Staying inside the parabola: I asked them to work on it, but then switched to an open discussion. This worked in the context, and got quite a few different participants chipping in, but it might have been better to have them explain it to each other for a while.
I say it is an argument by contradiction; but this is not quite right, is it?
3.2 Further uses of the Isoclines Mathlet
There are many other things you can ask your students to think about using the Isoclines Mathlet. Below, I will state three observations you can make using this Mathlet.
After stating each observation, I will offer hints you can share if your students need them. I will also provide some answers that students have come up with. Remember that students will come up with various ways to phrase arguments for these facts. The following provides a few of my own descriptions along with some alternatives to help you be better prepared to offer some ideas about suggestions to groups that get stuck.
- First Observation: Once an integral curve enters the region to the right of the isocline, it is trapped in that region forever (for all larger
). Appearances can be deceiving, though. Is this really true? To be sure, you have to come up with an argument for it.
- Hints:
- Point out that there are curves that cross this parabola from the inside. Why can they not be integral curves?
- Invite students to consider the slope of the tangent line of the parabola at the point of crossing.
- Answers:
- Curves can certainly cross this parabola moving from inside to the outside (as you move to the right). But these cannot be integral curves.
- When an integral curve crosses the nullcline, it must cross with slope zero, and horizontal lines always cross from outside to inside, never from inside to outside.
- Hints:
- Second Observation: If an integral curve goes through some point directly below the lower branch of the nullcline (so for some
,
, then it will cross the nullcline somewhere further to the right. Is this really true? To be sure, you have to come up with an argument for it.
- Hint:
- Draw a horizontal straight line through the chosen point.
- Answers:
- Below the nullcline the slopes are positive; so, until it crosses the nullcline, the solution stays above a horizontal line; but every horizontal line crosses the nullcline eventually, so the integral curve has to also.
- Hint:
- Third Observation: Many solutions become asymptotic to the lower branch of the nullcline as
. Is this really true? To be sure, you have to come up with an argument for it.
- Hints:
- This is tricky. Invite students to consider the
isocline. If that does not help your students recognize a solution, ask them whether solutions can ever cross it from below.
- This is tricky. Invite students to consider the
- Answers:
- One way to see this is to focus on an isocline for some negative slope; say
. This is another parabola, nested inside the nullcline. The two are asymptotic as
(because
as
).
- It looks as though an an integral curve cannot cross the lower branch of the
isocline from the outside of that parabola. That would trap the solution between the two parabolas, and show what we want.
- This is almost, but not quite true. Some solutions do cross from the outside. What is the dividing line? When an integral curve crosses the
isocline, it does so with slope
. If it comes from the outside, its slope must be greater than the (negative) slope of the tangent line to the isocline at that point. There are places where the slope of the tangent line is less than
; and at those points integral curves do cross from the outside. But eventually the slope of the tangent line to the
isocline become greater than
, and from then on the integral curves cannot cross from the outside. (Using calculus you can see that this occurs at
.)
- So if a solution
has
, then it never crosses the
isocline. It is trapped between these two isoclines, and so asymptotic to both.
- One way to see this is to focus on an isocline for some negative slope; say
- Hints:
3.3 Segment 1 Conclusion
There are many other questions stimulated by the Isoclines Mathlet. If you want students to find reasons for them, you had better have a reason in mind yourself! For example, it seems clear enough from the Mathlet that every integral curve falls into one of the following three categories, according to its behavior for large .
- The integral curve is asymptotic to
(from above) as
.
- The integral curve is asymptotic (from the left) to a vertical straight line
so the solution fails to exist for large
.
- The integral curve is asymptotic (from above) to
as
.
The third option has just one member, the separatrix, which separates the other two behaviors from each other.
Also, all integral curves are asymptotic from the right to a vertical straight line (as becomes smalls).
Some parts of this picture are elementary, but some are harder to prove.
Curves which integral curves can cross from only one side are called fences. Portions of isoclines often form useful fences; but in principle any curve can form a fence. For example, escape of solutions to infinity can be verified using appropriate fences that are asymptotic to vertical lines.
Pairs of fences that trap solutions are called funnels.
4. Mathlets in Group Work, Segment 2
Segment 2 introduces the concept of Mathlets in Group Work and provides ideas for setting up group work in your course.
Transcript [ PDF ]
Next I provide a couple examples of group work projects involving various Mathlets that could be incorporated into your courses.
4.1 First Project: Beats and the Complex Exponential
This exercise would be appropriate in a class in which the complex exponential plays a big role.
Launch
Mathlet: Beats
The various formulas on the screen indicate that the green curve in the top window is the graph of the sum of the two sinusoidal functions represented by the red and yellow curves in the bottom window. The [zoom] button lets you get a closer look at these graphs. Here are some questions for you to think about.
- What is the angular frequency of the red sinusoid? What is the significance of the parameter
? How about
?
?
- Zoom out and set
(or any other number near to 1). Describe in words what you see on the top screen.
- Assume that
and
. Use a trigonometric identity to express the function represented by the green curve in terms of trigonometric functions. Does the result explain what you see? Invoke the [Envelope] key now. Describe what the word envelope signifies, and write down the functions whose graphs give the envelope in this case.
- Still assuming that
, watch what happens when
is decreased from
to
. Pick a nonzero value of
and watch what happens as
is increased. Here is the challenge: Find a formula for the functions whose graphs are the envelope, for general
.
To get you started, it is a good idea to write
and use properties of the complex exponential.
Comments
Solutions to the project can be found on the theory page of the Beats Mathlet. In setting up this project, I tried to begin by encouraging exploration of the Mathlet.
Think About
What are your comments about the Beats project? Identify the parts of this project that will be useful in one of the classes you teach.
4.2 Second Project: Riemann Sums
Launch
Mathlet: Riemann Sums
A menu selects the function whose graph is drawn. The function is approximated by a step-function, whose integral is read out as Estimate. Various checkboxes produce different approximations.
- Accept the default function,
, and the default choice of left endpoint evaluation. Let the Mathlet compute the estimates for the integral with
rectangles, where
.
- Based on your findings in (1), do you have a prediction for the actual value of the integral? Compute the integral explicitly using an anti-derivative. Compare results.
- Now select [Min]. This constructs an approximation using the minimal value of
in each interval, as you can see by choosing fairly small values for
. What happens to the estimates as
increases? Please explain your observation. Can you predict what the trend is of the estimates using the maximum values in each interval? Check it on the Mathlet.
- Return to the [Evaluation point] selection, and use the slider which appears next to that checkbox to vary the point at which the function is evaluated. What is the trend as
gets large, using left endpoint evaluation? How about for right endpoint evaluation? Can you explain what you observe?
- Now select [Simpson’s Rule]. What is the trend now? Please explain!
Comments
The goals here are to get students to think about the various different ways to approximate an integral, and to see that (for this function, at least!) they all lead to the same result. Of course Simpson’s method gives the correct answer outright because it is approximating a parabola by a parabola. This project could be continued by asking about the rate of convergence. In all the menu items, Simpson’s rule appears to give the exact answer for very small . The read out [Estimate] shows that this is not true, though, and students could be asked to see that the errors are quadratic for Simpson’s rule and linear for any of the other approximations. It may appear that the trapezoidal rule should be better than the yellow approximations, but the Mathlet shows that this is not so, and a good project is to explain why it is really a first order scheme.
Think About
What are your comments regarding the Riemann Sums project? Include a few ideas for ways that this all or part of this project could be incorporated into a course you teach. Are there any changes that you will make to meet your needs of your course?
4.3 Segment 2 Conclusion
I now leave you with my parting thoughts regarding the use of Mathlets during group work.
Transcript [ PDF ]
5. Post-Module Activity
Exercise
Practice writing instructions for group work using Mathlets. These instructions might be verbal or the might be a written script. In any case, begin with a specification of the context (what point in what course) and learning objectives; then give the group work instructions.
Pick two of these three options:
- Pick any one of the Further questions mentioned in the discussion following Module 2, Session 1, in connection with Isoclines, and design some group work around it. Alternatively: pick a different menu item from Isoclines and write out a group work project.
- Trigonometric Identity is very simple, but still a lot of fun. Notice that green is blue plus yellow. You could play a game with this: Player Alice sets A and
, and Player Bob has to match the red curve with the green one by adjusting the a and b sliders. The key of course is the trigonometric identity reflecting the fact that if
are the polar coordinates of
then
. Design a group work project around this Mathlet.
- Pick another Mathlet and design a project around some part of it.
These materials are Copyright © 2013, Massachusetts Institute of Technology and unless otherwise specified are licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported license.