Module 1

Module 1: Mathlets in Lecture

This module contains two examples of the use of the MIT Mathlets in lecture. The first illustrates the artistic and dynamic character of the Mathlets. The second and more interactive example shows how formulas can be brought to life using the Mathlets in lecture. Each segment is followed by an opportunity for you to discuss this material on the Discussion Forum, and some remarks of my own about the lecture fragments and the features of the Mathlets and their use that are illuminated by these examples. At the end there are a couple of exercises for you to complete.

1. Outline

Each module will begin with an outline that is provided to serve as your guide through the modules online content.

The Outline for Module 1 includes the following:

Outline
Learning Objectives
Mathlets in Lecture, Segment 1
- Video of Lecture use of Linear Phase Portraits Cursory Entry Mathlet
- Discussion Questions
- Discussion of Segment 1
- Conclusion
Mathlets in Lecture, Segment 2:
- Video of Lecture use of Graph Features Mathlet
- Discussion Questions
- Discussion of Segment 2
- Conclusion
Exercises
Resources

2. Learning Objectives

After completing this module, the participant will be able to use Mathlets to:

Support lecture-based instruction.
Increase student participation in the lecture.
Use Mathlets to help students correlate visual images with symbols and computations.

3. Mathlets in Lecture, Segment 1

Welcome to the first of three modules included in our Mathlets: An Introduction course. During this module, we will interact with each other using pre-recorded video lectures, and interactive activities that will require you to interact with your peers by posting responses in the discussion forums located within the online course room.

All of the activities incorporated into our sessions are designed to extend your learning experience and provide an opportunity to learn from and with your peers, as well as your instructor.

In this video clip, I will introduce the first Segment of this Module, set out its learning objectives, and make some general comments about using Mathlets in lecture. Then you will watch a fragment of a lecture centered on the Linear Phase Portraits: Cursor Entry Mathlet. This is followed by a brief discussion of the lecture, and some questions for you to consider and answer in the Discussion Forum.

As you watch the Mathlets in Lecture, Segment 1 video, take notes regarding the following:

Your reactions to the Mathlets.
Thoughts about how you would or will incorporate the Mathlets into your own teaching.
Thoughts about the approach you would use to teach the material presented.

Prior to starting the video, please click the link provided to open the Mathlet used during this video segment: Linear Phase Portraits Cursor Entry Mathlet

Download the transcript for the Mathlets in Lecture, Segment 1 video. When you are ready, click play to begin the video segment.

Discussion Questions

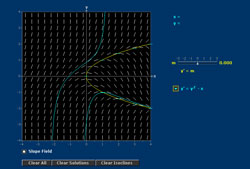The video segment you just completed ended with the presentation of three sets of questions for you to reflect and respond to. The first is regarding your initial thoughts and reactions regarding the Mathlet applets. Next, I want you to reflect on how I introduced the Mathlet applets versus how you would approach the same task, and finally please take a look to the future and all that you could do with the Mathlets.

Before you move on to read my comments, please take a few moments to post a response in the following discussion forums. Once you have posted your responses, please read and respond to two of your classmates posts.

After submitting your post to each of the three discussion forums, move on to the next section of this segment.

Module 1 Discussion Question 1: Introduction to Mathlets

Module 1 Discussion Question 2: Presenting Mathlet Functionality

Module 1 Discussion Question 3: Additional Investigations

Discussion of Segment 1

In an actual differential equations class, the objectives of a lecture fragment like this might be something like this:

Mathematical objectives:

- Demonstrate the variety of phase portraits afforded by homogeneous linear two-dimensional systems of differential equations.
- Demonstrate the control exercised by the trace and determinant of the defining matrix on the phase portrait.
- Convince the student that the trajectories deform smoothly as the matrix changes.

For a more mathematical audience I would have talked about the eigenvalues; they are together equivalent to giving the trace and determinant; whether they are complex or real determines the region in the trace-determinant plane; and the fact that the sign of the real part determines stability.

I also would have pointed out what is common among phase portraits of matrices with the same trace and determinant, at least in the case that the eigenvalues are real (nodes or saddles); this has to do with the relative magnitudes of the eigenvalues. For non-real eigenvalues $-$ inside the critical parabola $-$ the phase portrait consists of spirals. It is no longer the case that the space of matrices with given trace and determinant is connected. Instead, this space has two components, and that is represented by the split window. The upper part contains spirals that move in the clockwise direction; the lower part contains spirals that move in the counterclockwise direction.

The Mathlet used in this lecture has a cousin, Linear Phase Portraits: Matrix Entry. In this Mathlet, you can adjust the entries of the matrix A manually (by means of sliders, of course). One can also create the companion matrix, with top row [0, 1], with the given trace and determinant.

In my differential equations course, I use one or the other of these Mathlets in several different lectures, focusing on different aspects of it at different stages of our study of linear systems of differential equations.

Conclusion

To conclude this segment we will discuss the design features of the Mathlet applets. When preparing to teach using technology, it is important for you as the teacher to understand why the tool is designed the way it is. Finally, I will identify some of the advantages to using the Mathlet technology during your lectures that were identified during Segment 1.

Download the transcript for the Mathlets in Lecture, Segment 1 Conclusion video.

4. Mathlets in Lecture, Segment 2

Segment 2 provides an introduction to a more interactive approach to teaching with the Mathlets which is supported with research regarding active learning. During this segment of the video pay particular attention to and take notes regarding my interactions with the students in the workshop.

Prior to starting the video, please click the link provided to open the Mathlet used during this video segment: Graph Features Mathlet

Download the transcript for the Mathlets in Lecture, Segment 2 video.

Discussion Questions

Before you move on to read my comments regarding the first part of video Segment 2, please take a few moments to post a response in the following discussion forum. Once you have posted your responses, please read and respond to two of your classmates posts. Then you are ready to continue with the Segment 2 content.

Module 1: Discussion Question 4: Interactive Lecture

Discussion of Segment 2

It is a good exercise to analyze what the different objectives of a lecture are, at a pretty fine level. For example, here is a listing of the components of the lecture fragment about the Graph Features Mathlet.

Talking through what you see on the screen
Discussion of evaluation, set $x=0$
Graph features: rising, falling, concave, convex
Question: Control of behavior for large $z$ ?
More features: minima, maxima
First degree case
Second degree case
Question: What makes the graph go through the origin?
Question: What is the effect of increasing $b$ ?
Commentary on flash cards
Question: What is the role of linear term?
Completing the square
Checking the result
Getting more from the formula: effect of $b$
…And verifying it on the Mathlet

Here are some comments about this list.

One of the things the Mathlets let you do is break down the lecture into small fragments. This keeps the students interested, and lets them pick up the thread after attention lapses.

I decided to begin by accepting the rather interesting graph of the cubic, but to ask a question which reverses the usual sequence: instead of starting with the formula for our function and asking what can be said about the graph, I started with the graph and asked how you had to adjust the coefficients to achieve particular effects: behavior for large $x$ , and behavior for $x=0$ .

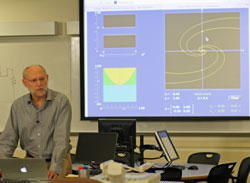While I was lecturing, I was inviting students to help me perform the demonstration. So, for example, as soon as a student proposed reversing the sign of $a$ to make the function decrease for large $x$ , I accepted it and tried it out on the Mathlet. This is a good example of how you can perform experiments in class with the Mathlets.

I decided to pose this question before talking about other graph features, critical points and point of inflection, to break up the descriptive part of the talk a little bit.

I invited a vote about the effect of increasing $b$ . This is a concept quiz. By chance, the camera picked up one of the virtual votes I was referring to in my lecture. You can see the hand go up and then quickly down again, in the back of the room. A number of participants thought that increasing $b$ would make the parabola fatter. They put up their hands in support of fatter, but when the saw they were in a minority they quickly put their hands down again. I think the sense of shame (surely undeserved!) probably negated any learning they might have experienced.

I said that asking about the role of the linear term was unfair. Well, whether it is unfair or not depends upon the context. If I want students to exercise their skill at completing the square and interpreting the result, or taking the derivative and setting it equal to zero, this would be a perfectly appropriate question. But these were not skills I wanted to challenge this audience with in this particular lecture fragment.

Conclusion

To conclude Mathlets in Lecture, Segment 2, I will provide a few useful hints on using the Mathlet applets in your lectures, and discuss the use of concept questions. Finally, I will once again identify some of the advantages to using the Mathlet technology that were identified during this segment.

Download the transcript for the Mathlets in Lecture, Segment 2 Conclusion video.

5. Exercises

Click the Module 1 Exercises link for the instructions and requirements for this module’s Exercises. Note that these ungraded exercises are designed to help enhance and guide your reflection on the learning of the content presented.

Module 1 Exercises

6. Resources

All Mathlets presented in this module along with additional resources are available on the Mathlets.org web site. Take some time to familiarize yourself with the resources available on the web site.

Provided here are quick links to access the Mathlets.org web site, as well as the applets presented or referenced in the video segments of this module.

Also provided are a downloadable copy of the full module video, the slides presented in the video, and the video transcripts.

Additional Resources

Mathlets in Lecture (Slides, PDF)